
How to report the results of public health research
“What can be asserted without evidence can also be dismissed without evidence.”—Christopher Hitchens [1949–2011], British journalist and writer (1).
Introduction
Science depends on measurement, and the end-products of measurement, in most instances, are numbers. These numbers are then combined and analyzed to produce meaningful results. To publish their research findings, researchers, like it or not, must have a good command of the ways results are correctly reported in the literature. Established rules can help communicate statistics effectively. Here, I present several important points to be considered when reporting results in manuscripts submitted to public health journals or biomedical journals.
Reporting numbers
Dozens of rules govern how numbers are reported in scientific papers (2). The rules given here are common and can be followed when writing a scientific paper, unless the journal’s instructions for authors specify a different set of rules.
Numbers less than 10 should be spelled out, unless they are units of measurements or time, which are always reported as numerals. For example, “In the study group, nine patients had fever.” But, “In the control group, 12 patients had anemia.” Furthermore, a sentence should not start with a number. For example, we should write, “Twenty-four patients were included in the study.” Consider a sentence beginning with a number like 23.45%! Instead of writing “23.45% of nucleotides sequenced…” we would have to write “Twenty-three and forty-five hundredths of a percent of nucleotides sequenced…” This problem can be avoided by rewording the sentence so that it begins with a word (3). Some authors begin such sentences with words or statements such as “Overall,” or “A total of…” to avoid this problem.
These are general rules, but sometimes we have to override them. When two numbers appear together, it might be better to spell out one of them. For example, the sentence, “In the laboratory, 11 250-mL aliquots of the sera were analyzed,” it would be better to write “In the laboratory, eleven 250-mL aliquots of the sera were analyzed.” If you find the numbers confusing, follow the general rules mentioned above.
Reporting numbers with full precision may not always be necessary for several reasons. For example, although in a table we may report that the annual hospitalization cost was “US$ 72,583,” in the Discussion, it may be better to say that the annual hospitalization cost was “almost US$ 73,000” because we process numbers most effectively when they have at most two significant digits, and rounding 72,583 to 73,000 would improve comprehension and recall of the number (3,4).
Rounding is not always appropriate, however. For example, terminal digit bias is the tendency of people to round to the nearest 0, even number, or 5. In one study (5), changing the definition of hypertension from a systolic blood pressure of “greater than or equal to” 140 mmHg to only “greater than” 140 mmHg decreased the prevalence of hypertension from 26% to 13%!
Errors in simple math are a BIG problem in the literature. Such errors often originate from bugs in software programs used for data analysis (6), but many are careless mistakes in arithmetic, a problem noted for decades (7). Sometimes, when authors submit a revised version of their manuscript to the journal, they forget to change all mentions of the same numbers—for example, although the data in the Results section may have been changed, the corresponding data in the Abstract and Tables may not have been.
Reporting percentages
Whenever you report a percentage, the numerator and denominator should be readily apparent. For example, instead of “We observed acute graft rejection in 24.66% of transplant recipients” it is better to write, “We observed acute graft rejection in 18 (24.66%) of 73 transplant recipients.” However, here we come to another important aspect of reporting numbers—the precision with which they should be reported. Aristotle once said “It is the mark of an educated mind to rest satisfied with the degree of precision which the nature of the subject admits and not to seek exactness where only an approximation is possible” (8). As a rule of thumb, when the number of the denominator is less than 100, it is better to report percentages only as whole numbers (3,9,10). In our example, because the total number of recipients (n=73) is less than 100, the correct version of the sentence would be “We observed acute graft rejection in 18 (25%) of 73 transplant recipients.” The reason is obvious; when the denominator is less than 100, an increase or a decrease of one unit in the numerator corresponds to a greater than 1% increase or decrease in the calculated percentage (for our example of 73 patients, 1.4%), respectively (9). When the denominator is less than 20, it is better not to report percentages at all, as they are easily misleading (11,12). The statement that “the new drug resulted in 50% survival of patients with an incurable disease” would be impressive, until we learn that the total number of patients treated was only two—one died and the other was alive at the time of report!
95% confidence intervals (95% CI)
Another way to express the precision of a result, say a percentage, is to present it with a 95% CI. For example: what is the difference between the percentages in the statement, “The prevalence of brucellosis was 30% in Shiraz,” when it is used by two researchers in separate articles? The first researcher studied 100 students and found 30 of them to be seropositive for the disease. The second researcher studied 10,000 students and found 3,000 of them to be seropositive. The statement is true for both studies, but you intuitively know that the 30% reported by the second researcher is more precise than the 30% reported by the first researcher, even if you do not have any idea what the exact meaning of 95% CI is. Adding a CI to the above statement for the first researcher, we have “Of 100 veterinary students examined, 30 were seropositive for brucellosis, translating into a prevalence of 30% (95% CI, 21–39%).” The statement for the second researcher would be “Of 10,000 veterinary students examined, 3,000 were seropositive for brucellosis, or a prevalence of 30.0% (95% CI, 29.1–30.9%).” This value for the second researcher (although it is exactly the same as that of the first) however, is written as 30.0% (with a zero after the decimal point), indicating the precision in its derivation. The two statements also differ in the reported 95% CIs; the first 95% CI of 21–39% means that if similar studies (each examining samples of 100 students from the population) had been conducted, say 1,000 times, the variability of random sampling would have resulted in prevalence rates between 21% and 39% in 95% of studies—that is, in 950 of 1,000 studies conducted. In other words, the prevalence in the studied population with a probability of 95% is between 21% and 39% (the width of this interval is 39%−21%=18%).
A similar argument is true for the second study. Here, the 95% CI is narrower (the width is 30.9%−29.1%=1.8%), reflecting a more precise estimate of the prevalence, as expected considering the larger sample size of 10,000 students. In fact, the precision of the measurement is 10 times (18/1.8) that found in the first study. This observation illustrates an important basic statistical rule: to achieve a tenfold increase in precision, we need to increase the sample size by a hundredfold (10,000/100), keeping other things constant (9). Therefore, reporting the 95% CI is recommended whenever we report percentages or any other effect size, particularly when the result is a primary or secondary outcome.
Reporting CI also keeps readers’ attention focused on the biology of the effect size (say, the reported difference between groups) and away from the P value, which is a mathematical indication of chance as the cause of the difference. For example, consider the sentence, “The drug significantly reduced diastolic blood pressure by a mean of 15 (95% CI, 3.5–26.5; P=0.01) mmHg.” Here, this single study found a statistically significant drop of 15 mmHg in diastolic blood pressure, which could be clinically important. However, the expected observed drop would range from 3.5 to 26.5 mmHg in 95 of 100 similar studies with the same sample size taken at random from the same population. Although a drop of 26.5 mmHg is clinically important, a drop of 3.5 mmHg is not. Thus, the study is clinically inconclusive, despite being statistically significant. When the 95% CI includes only clinically important (or only clinically unimportant) values, we have a more definitive conclusion about the effect of the treatment.
Reporting descriptive statistics
The mean and standard deviation (SD) should be reported with the precision (or one more decimal point) used in measuring the raw data (9,13). This degree of precision, in fact, should reflect the clinical importance of the measurement. For example, in clinical practice, although a change of merely 0.01 in blood pH is clinically important, a change of 1 mg/dL in serum cholesterol concentration is not. We therefore measure (and report) blood pH with two digits after the decimal point, say 7.39, and serum cholesterol concentration as an integer, say, 142 mg/dL. We therefore write, “The mean (SD) blood pH was 7.23 (0.09)” and “The mean (SD) serum cholesterol level was 201 [110] mg/dL.”
We use SD, not standard error of the mean (SEM), to reflect the dispersion of data around the mean (3,10,12). The SEM is always less than the SD, and some researchers intentionally use it to imply a lower variability (i.e., more precision) in raw data measurements. However, many journals, mostly in the basic sciences, expect or allow authors to summarize their data as means and SEMs, which technically are not descriptive statistics.
Reporting a variable with the mean and SD, is, however, only appropriate when the distribution of data is normal (Gaussian). In a normal distribution, about 68% of data are included in the interval defined by 1 SD above and below the mean, and 95% are included in the interval between 2 SDs above and below the mean. However, these relationships are only true when the data are normally distributed. When they are not, reporting the mean and SD is misleading.
One simple rule that suggests that the data may not be normally distributed is to see whether the SD is greater than half of the mean value. For example, in the above example, the SD for cholesterol concentration (110 mg/dL) is more than half of the mean concentration (201 mg/dL). This difference suggests that the variable cholesterol is not normally distributed and thus reporting it as a mean and SD would be inappropriate (3,10,12). “Skewed” or non-normally distributed data should be reported as medians and interquartile ranges (IQR), or the range of values that include the middle 50% of the data. The above statement is thus better written as “The median (IQR) serum cholesterol level was 140 (120 to 250) mg/dL.” The mean and SD are more commonly reported than the median and IQR. However, most biological variables are not normally distributed, so the median and IQR should be used far more often than they are.
The precision to be used for reporting median and IQR is similar to what has been mentioned for mean and SD. Further details on how precise a statistic should be reported are elaborated elsewhere (14).
Reporting P values
The most common statistic reported in scientific papers is a P value. The idea, introduced to help scientists, has since become a pain in the neck because the concept is often misunderstood and incorrectly used and interpreted (15,16). For example, the sentence “The mean (SD) hemoglobin concentration was 13.1 (1.1) g/dL in men, which was significantly higher than that in women [12.5 (0.8) g/dL; P=0.04]” implies that, assuming the null hypothesis, had the baseline distributions of hemoglobin concentrations in men and women been similar (equal means, equal SDs, same shapes, etc.), the probability of observing a difference between the means of the two samples of 0.6 g/dL or greater (13.1−12.5=0.6 g/dL) would be 0.04 (17,18). That is, even if the intervention was ineffective, the mean hemoglobin concentrations would be expected to differ by 0.6 g/dL or more in 4 of 100 similar studies. By convention, the difference is considered to be “statistically significant” if the P value is less than the “alpha level” that defines statistical significance, which is usually set at 0.05. This 5% willingness to be wrong is the risk we take when we believe the observed difference exists in the population, when it really does not—the so-called “type I” or “alpha error” (3,12).
In medical writing, the word “significant” is used only in its statistical meaning. To describe important differences that are not statistically significant, words such as “markedly” or “substantial” are preferred. Furthermore, although traditionally a significant P value was reported as “P<0.05,” nowadays, most journals prefer to see the exact value (as in our example above). In most instances, it is enough to report the value to two significant digits after the decimal point, unless the value is close to 0.05 or less than 0.001. However, many statistical software programs report P values to three decimal places. For example, a P value of “0.00023” is reported in the printout as “0.000.” Some authors erroneously report this value exactly as “P=0.000” or worse “P<0.000”! A P value is a probability; it cannot be negative, thus “P<0.000” is incorrect. On the other hand, the experimental nature of our studies means that no researcher can be 100% sure about their findings—there are always traces of doubts and uncertainty in results obtained (3,12,13). In such instances, we should write “P<0.001”.
Statistical significance should not be mistaken for clinical importance. Statistical significance depends on the study sample size, among other things. In a well-designed study, the sample size is calculated to detect the minimum clinically important difference, so that the clinical importance and statistical significance become equivalent—what is clinically important is also statistically significant and vice versa.
The multiple comparisons problem
Another statistical concern is the multiple comparisons problem, which can occur when many P values are calculated from the same dataset. The problem arises, for example, when more than two groups are compared with hypothesis tests, when testing multiple endpoints influenced by the same explanatory variables, or when one endpoint is measured at several occasions over time (which is often done in studies involving potentially harmful effects).
Each hypothesis test carries a risk of type I error. The more comparisons, the more likely we are to make a type I error: attributing a difference to an intervention when chance is the more likely explanation. For example, to compare means of a normally distributed variable, say age in three groups, we may choose to use the appropriate test; that is, one-way analysis of variance (ANOVA), or we may choose Student’s t test for independent samples to compare groups 1 and 2, groups 1 and 3, and groups 2 and 3—a total of three “pair-wise” comparisons, which would increase the risk of type I error. The number of tests necessary for comparing pairs of groups increases rapidly with increasing number of groups, so that for comparison of 6 groups, 15 statistical pair-wise tests are necessary. This many tests would increase the probability of type I error from 0.05 to 0.54!
One way to compensate for multiple comparisons (besides using an appropriate statistical test) is using the Bonferroni correction; that is, to change the commonly used threshold value for statistical significance of 0.05 to 0.05/n, where n is the number of comparisons to be made. In this way, the cut-off for 15 comparisons necessary for pair-wise comparisons of the means of 6 groups would be 0.003 (=0.05/15)—only P values less than 0.003 would be considered statistically significant. Thus, a P value of 0.04 would no longer be statistically significant in this example (3,17,18). The Bonferroni correction, although easy to understand, is no longer the preferred adjustment. Many other corrections for multiple comparisons have been developed, such as Scheffe’s test, Student-Newman-Keuls test, Tukey test, and Holm test, to name only a few of tests in this group (17). A detailed discussion of these methods is beyond the scope of this short article.
In addition to P values, other statistics may need to be reported about a hypothesis test. The earlier example could be written as “The mean (SD) hemoglobin concentration was 13.1 (1.1) g/dL in men, which was significantly higher than that in women [12.5 (0.8) g/dL; t=2.69, df=47, P=0.038].” In this case, the “test statistic” (t=2.69), which is the outcome of the statistical test, and the “degrees of freedom” (df=47), which identifies the probability distribution used to determine the P value, are also reported. Although all journals should encourage complete reporting of statistical analyses, many unfortunately do not, despite established reporting guidelines (3,13).
The P value depends on the difference observed between the two groups (also referred to as the “effect size”) and is a function of the sample size and other variables. Therefore, a smaller (more significant) P value cannot always be interpreted as being associated with a larger effect size. A significant P value can only indicate how likely the observed difference is to be caused by chance under the null hypothesis. Consider the following statement describing the above example on hemoglobin concentration: “The mean (SD) difference in hemoglobin concentration was 0.6 (95% CI, 0.03–1.18) g/dL higher in men than in women [13.1 (1.1) vs. 12.5 (0.8) g/dL].” Here, there is no P value, but from the 95% CI of the difference (0.6 g/dL), which does not include zero, we learn that the observed difference is significant at the level of 0.05 (because we used the 95% CI). Many biomedical and public health journals now require 95% CIs, either instead of, or in addition to, P values because CIs are more informative than the P value—they not only indicate statistical significance, but also present the magnitude of the estimated difference, which allows the clinical importance of the difference to be examined.
Reporting risk
Risk is commonly reported with a risk ratio (RR), especially in cohort studies, an odds ratio (OR), in case-control studies and sometimes in cross-sectional studies, the absolute risk reduction (ARR), also referred to as attributable risk, a hazards ratio (HR), mostly reported in survival or time-to-event analysis, the number needed to treat (NNT), or the number needed to harm (NNH). These statistics should be presented with 95% CIs. As mentioned earlier, when the 95% CI is presented, the associated P value does not need to be reported because it does not provide further information. That is, when the 95% CI for a RR, OR, or HR does not include 1 (indicating equal risk), the ratio is statistically significant at the 0.05 level.
The above-mentioned statistics are either calculated in univariate (or unadjusted) analysis as crude ratios (e.g., a crude OR), or they are derived by more complex analyses adjusted for the effects of other variables, say, with logistic regression analysis (to produce an adjusted OR) or Cox regression analysis (to produce an adjusted HR). Examples of correct usage of RR, HR, NNT, and NNH are “Smoking was associated with a higher risk of lung cancer (RR, 3.5; 95% CI, 2.0–6.1)”; “Chemotherapy was associated with a higher 5-year survival rate (adjusted HR, 0.07; 95% CI, 0.01–0.53);” and “The NNT for preventing one additional death (52; 95% CI, 33–124) was lower than the NNH to incur one additional serious adverse drug reaction (131; 95% CI, 55–1,500).”
When any of the above indices are reported, the absolute risk should also be reported because they are all calculated from the absolute risk, and their interpretation would be misleading without considering the absolute values. For example, we might be impressed to read “The treatment decreased disease mortality by 67%.” However, our surprise vanishes when we learn that “The mortality was decreased from 3 in 1,000 to 1 in 1,000 people with the disease.” This difference corresponds to an ARR of 0.002 and a NNT of 500; that is, to save one person, 500 people would need to be treated (19)!
Reporting diagnostic tests
Two important issues are common in reporting the results of diagnostic tests and predictive or prognostic studies—comparing the performance of a new (or an index) test with that of a reference test (the standard test), and assessing the level of agreement between two or more tests. When an index test is compared to a reference test, we usually report the sensitivity, specificity, and positive and negative predictive values, along with their 95% CIs (3,19). For example, we may write “Using the pathologic results as the reference standard, a C-reactive protein concentration greater than 123 mg/L, as a test for diagnosing cholecystitis, had a sensitivity of 83% (95% CI, 76–89%), a specificity of 93% (95% CI, 89–96%), a positive predictive value of 89% (95% CI, 83–93%), and a negative predictive value of 89% (95% CI, 85–92%).” Sometimes, other diagnostic performance indices, such as positive and negative likelihood ratios or the number needed to misdiagnose (the number of tests that will be performed for each wrong result) along with their 95% CIs are also reported (20,21).
Another important test index, also reported with a 95% CI, is the area under the receiver operating characteristics (ROC) curve (Figure 1). The area is equivalent to the probability that the test result measured in a randomly selected diseased person is higher than that measured in a non-diseased person (20). The test is informative (more accurate than tossing a coin!) if the 95% CI of the area under the ROC curve does not include 0.5. The higher the area, the better the test performance.
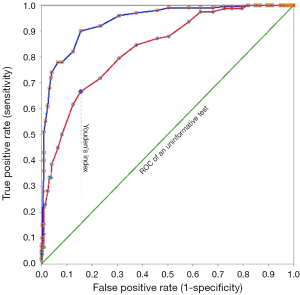
Of course, to present several such indices, it is better to present them in a table rather than in the text (Table 1). Another important point to report clearly is the value that defines a positive and a negative result—the cut-off value. In the above statement for example, a cut-off value of 123 mg/L was used. Reporting the normal range of a test is of little value because it only describes the distribution of test value in 95% of apparently healthy people and does not give any information about the distribution of values in patients (22).
Table 1
| Index | Value (95% CI) |
|---|---|
| Sensitivity | 66.7% (55.1–76.9) |
| Specificity | 84.5% (80.1–88.3) |
| Positive predictive value | 51.0% (43.5–58.4) |
| Negative predictive value | 91.3% (88.4–93.5) |
| Positive likelihood ratio | 4.3 (3.2–5.8) |
| Negative likelihood ratio | 0.4 (0.3–0.5) |
| Number needed to misdiagnose | 5.3 (4.3–6.5) |
There is a trade-off between the test sensitivity and specificity. Suppose a higher test value is associated with a higher probability of a disease. Increasing the test cut-off value decreases sensitivity and increases specificity (20). At a certain point, the sensitivity and specificity become equal (Figure 1). There are various criteria for determining the most appropriate cut-off value. For example, one tries to maximize the Youden’s index (Figure 1); another chooses the point where the test sensitivity and specificity are equal. In determining the most appropriate cut-off value, the assumptions should be clearly stated. The most appropriate cut-off value depends on the test properties (sensitivity and specificity), the costs and consequences (not only financial) associated with false-positive and false-positive test results (say, false positive results in breast cancer diagnosis can lead to unnecessary mastectomies, and false negative results in blood banks for HIV can contaminate the blood supply), as well as the prevalence of the disease of interest (20,23-25).
When we report how well two diagnostic test results agree, we have to report statistics showing the level of agreement—Cohen’s kappa (κ) and Krippendorff’s alpha (α), for example, along with their 95% CIs. These indices vary from –1 to +1. A value of zero indicates no agreement whereas values of +1 and –1 reflect “complete agreement” and “complete disagreement” between raters, respectively. Then, we may write, “The agreement of two radiologists for diagnosing sinusitis from radiographs was poor (Cohen’s κ 0.17; 95% CI, –0.71 to 1.00)” (26).
Agreement is not correlation. For example, suppose the reported serum glucose levels for three patients measured by two lab tests were 100, 150, 120; and 200, 300, 240 mg/dL, respectively. Although the two sets of results have a correlation of +1 (each reading in the second test is exactly twice that measured in the first test), there is no agreement at all between each corresponding reading.
Bayesian statistics: an alternative statistical approach
The value of the most common approach to statistics, known as frequentist statistics, has long been questioned by many researchers. The pre-defined cut-off of 0.05 for the P value means that a P value of 0.049 is statistically significant and that a P value of 0.051 is not. The two results are not so different, but that is the consequence of using frequentist statistics. In another school of statistical analysis, the Bayesian statistics, the story is far different.
Bayesian statistics is based on Bayes’ theorem, which describes the mathematical relationships between the prior or “pre-trial” probability of an event and the posterior or “post-trial” probability of the event, given the implications of the trial data (represented by the “likelihood”) (27,28). Simply put, the Bayesian method begins with a set of beliefs (the pre-trial probabilities) and then modifies these beliefs based on the data collected from a study (the likelihood), to form an updated set of beliefs, called the “post-trial probabilities.” That is, “Bayesian analysis determines how the results of a study change the opinion held before the study was conducted” (3).
The statistical methods section of the article
The statistical methods section appears at the end of the Methods section and describes how data were treated, how missing and outlying values were handled, how the normality of distributions was tested, what comparisons were made and with what statistical tests, and how the assumptions underlying each test were confirmed. The name and version of the software program used for data analysis should also be mentioned.
Furthermore, in the Methods section, the assumptions on which the minimum sample size was calculated should be clearly stated. As an example, we can write “Assuming an acceptable type I error of 0.05, an acceptable study power of 0.8, and an estimated SD of 12 mmHg in diastolic blood pressure, to detect a difference of 10 mmHg in mean diastolic blood pressure between two groups of equal size, we needed a minimum sample size of 46. Assuming a drop-out rate of 10% during follow up, 52 patients (26 in each treatment arm) were included in the study.” In the above statement, the “study power” is the probability (here, 80%) of detecting a statistically significant difference of at least 12 mmHg in the study when such a difference (or more) really exists in the population.
Final thoughts
Numbers have key roles in science and having something important to convey, a clear, comprehensible report of results can be the difference between a well-written manuscript acceptable for publication in a prestigious journal and a manuscript wandering around and being rejected.
Acknowledgments
I would like to express my gratitude to Tom Lang for his comments on a previous version of this manuscript.
Funding: None.
Footnote
Provenance and Peer Review: This article was commissioned by the the Guest Editor (Thomas A. Lang) for the series “Publication and Public Health” published in Journal of Public Health and Emergency. The article has undergone external peer review.
Conflicts of Interest: The author has completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/jphe.2017.12.02). The series “Publication and Public Health” was commissioned by the editorial office without any funding or sponsorship. The author has no other conflicts of interest to declare.
Ethical Statement: The author is accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Hitchens C. Mommie Dearest: The pope beatifies Mother Teresa, a fanatic, a fundamentalist, and a fraud. Slate October 20, 2003. (Accessed August 17, 2017). Available online: http://www.slate.com/articles/news_and_politics/fighting_words/2003/10/mommie_dearest.html
- American Medical Association. AMA Manual of Style: A Guide for Authors and Editors. 10th ed. New York: Oxford University Press, 2007.
- Lang TA, Secic M. How to report statistics in medicine: annotated guidelines for authors, editors, and reviewers. 2nd ed. Philadelphia: American College of Physicians, 2006.
- Lang T. The need to question terminal digits in scientific research. AMWA J 2013;28:141-2.
- Wen SW, Kramer MS, Hoey J, et al. Terminal digit preference, random error, and bias in routine clinical measurement of blood pressure. J Clin Epidemiol 1993;46:1187-93. [Crossref] [PubMed]
- Thimbleby H, Cairns P. Reducing number entry errors: solving a widespread, serious problem. J R Soc Interface 2010;7:1429-39. [Crossref] [PubMed]
- Davidson HA. Guide to Medical Writing. A Practical Manual for Physicians, Dentists, Nurses, Pharmacists. New York: The Ronald Press Company, 1957.
- The Quotations Page. (Accessed November 1, 2017). Available online: http://www.quotationspage.com/quote/3525.html
- Habibzadeh F, Habibzadeh P. How much precision in reporting statistics is enough? Croat Med J 2015;56:490-2. [Crossref] [PubMed]
- Habibzadeh F. Common statistical mistakes in manuscripts submitted to biomedical journals. European Science Editing 2013;39:92-4.
- Priebe HJ. The results. In: Hall GM. editors. How to write a paper. 3rd ed. London: BMJ Publishing Group, 2003:22-35.
- Habibzadeh F. Statistical Data Editing in Scientific Articles. J Korean Med Sci 2017;32:1072-6. [Crossref] [PubMed]
- Lang TA, Altman DG. Basic Statistical Reporting for Articles Published in Biomedical Journals: The “Statistical Analyses and Methods in the Published Literature” or The SAMPL Guidelines Int J Nurs Stud 2015;52:5-9. [Crossref] [PubMed]
- Karhu D, Vanzieleghem M. Significance of digits in scientific research. AMWA 2013;28:58-60.
- Mark DB, Lee KL, Harrell FE Jr. Understanding the Role of P Values and Hypothesis Tests in Clinical Research. JAMA Cardiol 2016;1:1048-54. [Crossref] [PubMed]
- Goodman S. A dirty dozen: twelve p-value misconceptions. Semin Hematol 2008;45:135-40. [Crossref] [PubMed]
- Glantz SA. Primer of Biostatistics. 5th ed. New York: McGraw-Hill, 2002.
- Spatz C, Johnston JO. Basic Statistics: Tales of Distribution. 4th ed. California: Brooks/Cole Publishing Co, 1989.
- Lang T. Odd cases and risky cohorts: measures of risk and association in observational studies. Medical Writing 2017;26:12-5.
- Habibzadeh F, Habibzadeh P, Yadollahie M. On determining the most appropriate test cut-off value: the case of tests with continuous results. Biochem Med (Zagreb) 2016;26:297-307. [Crossref] [PubMed]
- Habibzadeh F, Yadollahie M. Number needed to misdiagnose: a measure of diagnostic test effectiveness. Epidemiology 2013;24:170. [Crossref] [PubMed]
- Habibzadeh P, Yadollahie M, Habibzadeh F. What is a "Diagnostic Test Reference Range" Good for? Eur Urol 2017;72:859-60. [Crossref] [PubMed]
- Habibzadeh F, Habibzadeh P, Yadollahie M. Criterion used for determination of test cut-off value. Diabetes Res Clin Pract 2017;128:138-9. [Crossref] [PubMed]
- Sox HC, Higgins MC, Owens DK. Medical Decision Making. 2nd ed. Oxford, UK: Wiley-Blackwell, 2013.
- Newman TB, Kohn MA. Screening Tests: Evidence-Based Diagnosis. New York: Cambridge University Press, 2009.
- Bowers D, House A, Owens D. Understanding Clinical Papers. New York: Wiley, 2002.
- Goodman SN. Toward evidence-based medical statistics. 1: The P value fallacy. Ann Intern Med 1999;130:995-1004. [Crossref] [PubMed]
- Goodman SN. Toward evidence-based medical statistics. 2: The Bayes factor. Ann Intern Med 1999;130:1005-13. [Crossref] [PubMed]
Cite this article as: Habibzadeh F. How to report the results of public health research. J Public Health Emerg 2017;1:90.


